絶対値とは何か?──絶対値を正しく理解しよう
絶対値とは?
絶対値とは、数直線上でその数が原点(0)からどれだけ離れているかを表したものです。プラスでもマイナスでも、0からの距離を常に正の数で表します。つまり、絶対値とは「数の大きさ(距離)」を示すものなのです。
◆絶対値はプラスにすればいいだけ?
「絶対値って、マイナスの数をプラスにすればいいんでしょ?」 こんなふうに思ったこと、ありませんか?
たしかに、
\[|-5| = 5\]
のように、マイナスがプラスになっています。
でも、絶対値の本当の意味は、単なる「プラス化」ではありません。
今回は、そんな絶対値の定義を、やさしく、でもちょっとだけ深く見ていきましょう。
◆絶対値の正しい定義
まず、数学の世界での絶対値の定義を紹介します。
\[|a|=\begin{cases}
a & (a\ge0)
\\ -a & (a\lt0)
\end{cases}\]
【日本語での解釈】
この絶対値の定義は、 「\(a\)が\(0\)以上なら、そのまま」 「\(a\)が\(0\)より小さいなら、符号を変えて\(0\)以上にする」 というルールを意味しています。
もっと直感的に言うと──
- もともと\(0\)以上の数(たとえば\(5\)や\(0.2\)など)は、そのまま動かさずに。
- マイナスの数(たとえば\(-3\)や\(π-4\)など)は、その数全体にマイナスをかけて、\(0\)より大きい数に直してあげます。
つまり、絶対値とは、「数がどれだけ原点(\(0\))から離れているか」という距離を表すための道具なのです。
ポイント:
「式の一部分だけ」ではなく、「数全体(式全体)にマイナスをかける」という意識が大切です。
(例)\(|-3| = 3、|π-4| = 4-π\)
【まとめると】
- \(a \ge 0\) のときは、そのまま \(a\)。
- \(a < 0\) のときは、数全体にマイナスをかけて正の数にする。
この「\(0\)を境にした二通りの動き」が、絶対値の本質なんです。
◆絶対値がなぜこう定義されるのか?
絶対値がこのように定義される理由は、「距離」という考え方にあります。
【例】\( |π-4|\) を求めよう
\(π\)はおよそ\(3.14\)なので、\(π-4 ≈ -0.86\)となり、負の数になります。
ここで、数直線を思い浮かべてみましょう。
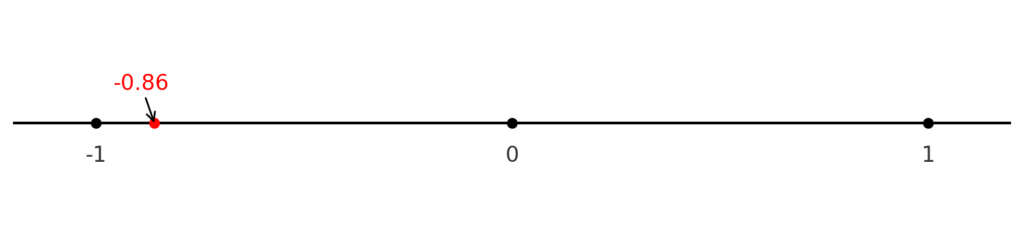
- 正の数は右側、負の数は左側に並ぶ数直線。
- \(π-4\)は\(0\)より少し左、つまり原点より左に位置します。
ここで、絶対値\(|π-4|\)を考えるときは、 今いる場所(負の数)から原点(\(0\))までの距離を求めます。
負の数なので、絶対値の定義にしたがって「数全体にマイナスをかけて」正の数に直します。
\[|π-4| = -(π-4) = 4-π\]
【ポイントまとめ】
- 負の数の絶対値は「数全体にマイナスをかける」。
- 絶対値とは「プラスに直す操作」ではなく、原点からの距離を求める操作。
◆絶対値の歴史 ~どのように生まれたのか~
絶対値の考え方は、古代ギリシャ時代にはすでに間接的に存在していましたが、 「絶対値」という言葉(absolute value)が登場したのは19世紀になってからです。
数直線や解析学の発展とともに、絶対値が重要な役割を担うようになりました。
まとめ ▶▶▶ 絶対値の見方を変えよう
もしあなたが今、数学に苦手意識を持っていたり、「公式を覚えるだけの学習」に限界を感じているなら、一度“理解する学び方”を体験してみてください。
数学本舗では、「わかるって、こんなに面白いんだ!」という体験を、誰にでも届けられるよう、丁寧な1対1のオンライン指導を行っています。
- 絶対値とは、数をプラスに直すだけのものではない。
- 絶対値とは、0からの距離を表している。
- 負の数の絶対値は「数全体にマイナスをかける」と考える。
- 「プラスにする」のではなく、「0以上にする」という意識が大切。
絶対値を意識するときは、「これは数直線上の距離を表しているんだな」とイメージしてみましょう。絶対値への見方がきっと変わるはずです!

📌 オンラインで、あなたのペースで学べます
数学本舗では、社会人・高校生を対象に、マンツーマンで丁寧な数学指導を行っています。
興味がある方はぜひお気軽にお問い合わせください!
👉 無料体験はこちら